Here’s a quick comparison of 3 different “low cost” temperature sensors:
This is how accurate they each claim to be:
| Model |
Accuracy in °C |
Accuracy in °F |
| TMP36 |
±2.00°C |
±3.6°F |
| Thermistor |
±0.45°C |
±0.8°F |
| DHT22 |
±0.50°C |
±0.9°F |
All the data below was collected with a BeagleBone Black which has a 12-bit ADC. The 10K thermistor was hooked up in a voltage divider configuration with a 1% 10K resistor. The DHT22 uses a thermistor inside as well, but has a digital output. Readings were taken every 3s over a 2 hour period.
The sensors are all positioned within 1/4″ of each other. The slow temperature drifts are from the house cooling and the furnace heating it back up.

Temperature
I used a running average filter with a window of 10 samples to clean up the noise a bit and these are the results.
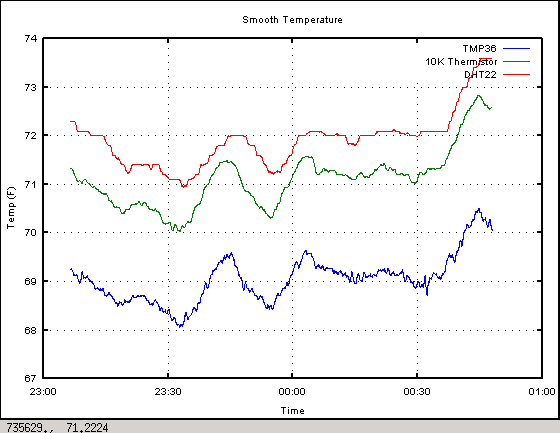
Temperature – 30s running average
Finally, taking the 10K thermistor as ground truth, these are the differences observed. The TMP36 is consistently about 2°F lower than the thermistor, and the DHT22 is roughly 1°F higher even though it’s also using a thermistor inside. I don’t know how accurate the ADC inside the DHT22 is, so that might explain some of the difference.
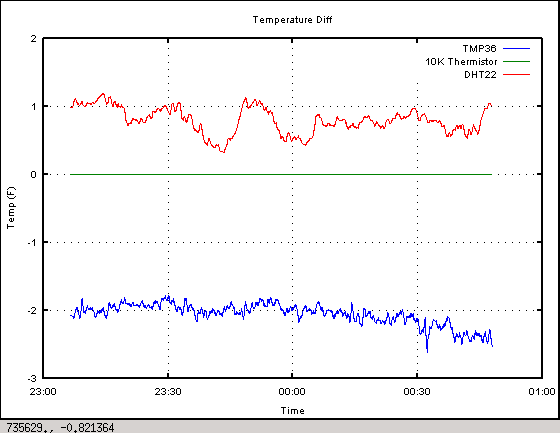
Deltas between different temperature sensors.
In conclusion, when you hear someone say “I keep my thermostat at 67°F” and another guy responds “My wife would kill me if I did that. I keep mine at 73°F” they might both be keeping their temperature at 70°F. It just depends on what temperature sensor their thermostat is using, and how well it was calibrated.
Simple reference card for tig, the text-mode interface for git.
This Tig Quick Reference Card shows all the key bindings supported by tig version 0.17.

Page 1

Page 2
The reference card is available as a PDF so you can print it out. The PDF version is derived from the TeX file which is hosted at http://github.com/gburca/git-qrc so anyone can update it.
In a previous post I showed how to analytically double integrate (or rather repeat integrate) a  wave to arrive at displacement or position. Here I’ll make it a little more generic, by integrating a sum of
wave to arrive at displacement or position. Here I’ll make it a little more generic, by integrating a sum of  waves, each with its own amplitude and phase. This exercise is motivated by the fact that any arbitrarily complex waveform can be expressed as the sum of a number of sinusoids, so this will allow us to obtain the exact displacement when the acceleration is arbitrarily complex, as long as we’re able to determine (through FFT perhaps) the sinusoids that make up the acceleration.
waves, each with its own amplitude and phase. This exercise is motivated by the fact that any arbitrarily complex waveform can be expressed as the sum of a number of sinusoids, so this will allow us to obtain the exact displacement when the acceleration is arbitrarily complex, as long as we’re able to determine (through FFT perhaps) the sinusoids that make up the acceleration.
We start with an acceleration defined as:
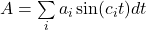
First integration, to obtain velocity:
(1) 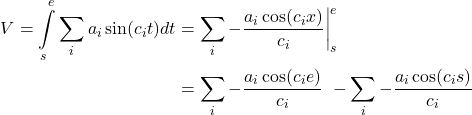
Let 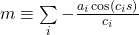 and then do the second integration, to obtain displacement or position.
and then do the second integration, to obtain displacement or position.
(2) ![Rendered by QuickLaTeX.com \begin{align*} D &= \int\limits_{g}^{h} \sum\limits_{i}{ - \frac{a_i \cos(c_i e)}{c_i}} \ - m\ de \\ &= \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2} - me \bigg|_g^h} \\ &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i h)}{c_i^2}} - mh \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i g)}{c_i^2}} - mg \right] \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-7d3277777343fb0ad9afd377e408b65a_l3.png)
Substitute everything back in (given 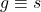 and
and 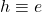 ), and simplify:
), and simplify:
(3) ![Rendered by QuickLaTeX.com \begin{align*} D &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i h)}{c_i^2}} - mh \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i g)}{c_i^2}} - mg \right] \\ &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2}} - me \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i s)}{c_i^2}} - ms \right] \\ &= \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2}} \ - \sum\limits_{i}{-\frac{a_i \sin(c_i s)}{c_i^2}} + (s-e)\sum\limits_{i}{ - \frac{a_i \cos(c_i s)}{c_i}} \\ &= \sum\limits_{i}{\frac{a_i \sin(c_i s)}{c_i^2}} \ - \sum\limits_{i}{\frac{a_i \sin(c_i e)}{c_i^2}} + (e-s)\sum\limits_{i}{\frac{a_i \cos(c_i s)}{c_i}} \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-1588dae166b76d154e41397796fe1f23_l3.png)
Finally, to take the phase of the signal into account, we would start with:
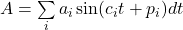
And end with:
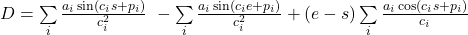
Recently I was trying to double integrate a sinusoidal acceleration (ex: a frog leaping forward) and was a bit puzzled at first why double integrating the 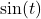 wave resulted in no displacement after an integral number of cycles:
wave resulted in no displacement after an integral number of cycles:
(1) 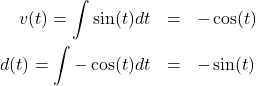
Everybody knows that integrating once gives you velocity, and integrating twice gives you displacement (or position). But if that’s the case, why is the displacement (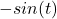 ) above sinusoidal? Shouldn’t the frog be moving forward instead of back and forth?
) above sinusoidal? Shouldn’t the frog be moving forward instead of back and forth?
It turns out my calculus was rusty enough to where I missed one very obvious fact. In the process I learned the distinction between a multiple (or double) integral, which is an integral taken over different variables (ex: 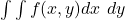 ) and a repeated integral which is taken multiple times over the same variable. What I missed was the difference between an indefinite integral (shown above) and a definite integral (shown below).
) and a repeated integral which is taken multiple times over the same variable. What I missed was the difference between an indefinite integral (shown above) and a definite integral (shown below).
So let’s make the problem a little more generic and add amplitude and frequency component to our acceleration signal, and then see what happens to it as we integrate it twice. We’ll start with an acceleration signal defined as:
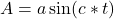
and we’ll integrate it twice over the interval start..end (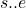 ) to see what we get.
) to see what we get.
For the first integration we have:
(2) 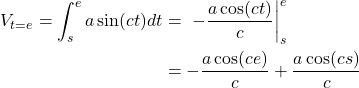
So that allows us to calculate the velocity at any point 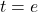 after the starting time
after the starting time  . Now we want to integrate a second time to get the displacement. To avoid confusion with the
. Now we want to integrate a second time to get the displacement. To avoid confusion with the 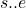 interval used for the first integration, we’ll use
interval used for the first integration, we’ll use 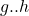 as the integration interval this time around. To simplify things, let’s also rename the integration constant (time independent) term
as the integration interval this time around. To simplify things, let’s also rename the integration constant (time independent) term  .
.
(3) ![Rendered by QuickLaTeX.com \begin{align*} D_{t = h} = \int_{g}^{h} -\frac{a \cos(ce)}{c} + m\ de &= -\frac{a \sin(ce)}{c^2} + me \bigg|_{g}^{h} \\ &= \left[ mh - \frac{a \sin(ch)}{c^2} \right] - \left[ mg - \frac{a \sin(cg)}{c^2} \right] \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-bf3a77e422710ba30f29c5dbcba02de2_l3.png)
Since both integrations are over the same intervals, we know that 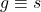 and
and 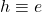 . Now substitute everything back in and simplify:
. Now substitute everything back in and simplify:
(4) ![Rendered by QuickLaTeX.com \begin{align*} D_{t = e} &= \left[ mh - \frac{a \sin(ch)}{c^2} \right] - \left[ mg - \frac{a \sin(cg)}{c^2} \right] \\ &= \left[ me - \frac{a \sin(ce)}{c^2} \right] - \left[ ms - \frac{a \sin(cs)}{c^2} \right] \\ &= m(e-s)\ - \frac{a \sin(ce)}{c^2} + \frac{a \sin(cs)}{c^2} \\ &= \frac{a \cos(cs)}{c} (e-s)\ - \frac{a \sin(ce)}{c^2} + \frac{a \sin(cs)}{c^2} \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-a56b2230a2b58f068f49180dac6d255b_l3.png)
If we want to take into account the phase of the signal, we start with:
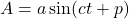
and end with:

So there you have it. The result of integrating a sinusoidal acceleration twice on the interval 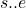 in order to arrive at the displacement.
in order to arrive at the displacement.
Here’s a solution if you ever get the following error when trying to delete the master branch in a remote repository:
remote: error: By default, deleting the current branch is denied, because the next
remote: error: 'git clone' won't result in any file checked out, causing confusion.
remote: error:
remote: error: You can set 'receive.denyDeleteCurrent' configuration variable to
remote: error: 'warn' or 'ignore' in the remote repository to allow deleting the
remote: error: current branch, with or without a warning message.
remote: error:
remote: error: To squelch this message, you can set it to 'refuse'.
remote: error: refusing to delete the current branch: refs/heads/master
To /somewhere/in/the/cloud/repo.git
! [remote rejected] master (deletion of the current branch prohibited)
error: failed to push some refs to '/somewhere/in/the/cloud/repo.git'
The reason you’re seeing the error is that HEAD on the remote repository by default contains something like this (see also line 9 in the error message above):
ref: refs/heads/master
If you have access to the remote repository, simply modify the HEAD file to point to a different branch and then you’ll be able to delete the remote master branch. There are some significant implications to modifying the remote HEAD, especially if other users are tracking that branch, so make sure you know what you’re doing if you choose to point it to some other arbitrary branch.





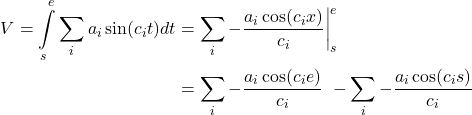
![Rendered by QuickLaTeX.com \begin{align*} D &= \int\limits_{g}^{h} \sum\limits_{i}{ - \frac{a_i \cos(c_i e)}{c_i}} \ - m\ de \\ &= \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2} - me \bigg|_g^h} \\ &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i h)}{c_i^2}} - mh \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i g)}{c_i^2}} - mg \right] \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-7d3277777343fb0ad9afd377e408b65a_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} D &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i h)}{c_i^2}} - mh \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i g)}{c_i^2}} - mg \right] \\ &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2}} - me \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i s)}{c_i^2}} - ms \right] \\ &= \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2}} \ - \sum\limits_{i}{-\frac{a_i \sin(c_i s)}{c_i^2}} + (s-e)\sum\limits_{i}{ - \frac{a_i \cos(c_i s)}{c_i}} \\ &= \sum\limits_{i}{\frac{a_i \sin(c_i s)}{c_i^2}} \ - \sum\limits_{i}{\frac{a_i \sin(c_i e)}{c_i^2}} + (e-s)\sum\limits_{i}{\frac{a_i \cos(c_i s)}{c_i}} \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-1588dae166b76d154e41397796fe1f23_l3.png)
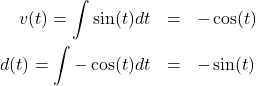
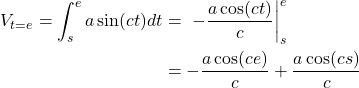
![Rendered by QuickLaTeX.com \begin{align*} D_{t = h} = \int_{g}^{h} -\frac{a \cos(ce)}{c} + m\ de &= -\frac{a \sin(ce)}{c^2} + me \bigg|_{g}^{h} \\ &= \left[ mh - \frac{a \sin(ch)}{c^2} \right] - \left[ mg - \frac{a \sin(cg)}{c^2} \right] \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-bf3a77e422710ba30f29c5dbcba02de2_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} D_{t = e} &= \left[ mh - \frac{a \sin(ch)}{c^2} \right] - \left[ mg - \frac{a \sin(cg)}{c^2} \right] \\ &= \left[ me - \frac{a \sin(ce)}{c^2} \right] - \left[ ms - \frac{a \sin(cs)}{c^2} \right] \\ &= m(e-s)\ - \frac{a \sin(ce)}{c^2} + \frac{a \sin(cs)}{c^2} \\ &= \frac{a \cos(cs)}{c} (e-s)\ - \frac{a \sin(ce)}{c^2} + \frac{a \sin(cs)}{c^2} \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-a56b2230a2b58f068f49180dac6d255b_l3.png)