Ebixio

From Acceleration to Displacement

May 27th, 2013 Gabriel Burca No comments

Recently I was trying to double integrate a sinusoidal acceleration (ex: a frog leaping forward) and was a bit puzzled at first why double integrating the $\sin(t)$ wave resulted in no displacement after an integral number of cycles:

(1) $\begin{eqnarray*} v(t) = \int \sin(t) dt &=& -\cos(t) \\ d(t) = \int -\cos(t) dt &=& -\sin(t) \end{eqnarray*}$

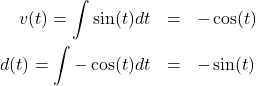
Everybody knows that integrating once gives you velocity, and integrating twice gives you displacement (or position). But if that’s the case, why is the displacement ( $-sin(t)$ ) above sinusoidal? Shouldn’t the frog be moving forward instead of back and forth?

It turns out my calculus was rusty enough to where I missed one very obvious fact. In the process I learned the distinction between a multiple (or double) integral, which is an integral taken over different variables (ex: $\int \int f(x, y) dx\ dy$ ) and a repeated integral which is taken multiple times over the same variable. What I missed was the difference between an indefinite integral (shown above) and a definite integral (shown below).

So let’s make the problem a little more generic and add amplitude and frequency component to our acceleration signal, and then see what happens to it as we integrate it twice. We’ll start with an acceleration signal defined as:

$A = a \sin(c*t)$

and we’ll integrate it twice over the interval start..end ( $s..e$ ) to see what we get.

For the first integration we have:

(2) $\begin{align*} V_{t = e} = \int_{s}^{e} a \sin(ct) dt &= \ - \frac{a \cos(ct)}{c}\bigg|_{s}^{e} \\ &= -\frac{a \cos(ce)}{c} + \frac{a \cos(cs)}{c} \end{align*}$

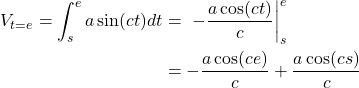
So that allows us to calculate the velocity at any point $t = e$ after the starting time $s$ . Now we want to integrate a second time to get the displacement. To avoid confusion with the $s..e$ interval used for the first integration, we’ll use $g..h$ as the integration interval this time around. To simplify things, let’s also rename the integration constant (time independent) term $\frac{a \cos(cs)}{c} \equiv m$ .

(3) $\begin{align*} D_{t = h} = \int_{g}^{h} -\frac{a \cos(ce)}{c} + m\ de &= -\frac{a \sin(ce)}{c^2} + me \bigg|_{g}^{h} \\ &= \left[ mh - \frac{a \sin(ch)}{c^2} \right] - \left[ mg - \frac{a \sin(cg)}{c^2} \right] \end{align*}$

Since both integrations are over the same intervals, we know that $g \equiv s$ and $h \equiv e$ . Now substitute everything back in and simplify:

(4) $\begin{align*} D_{t = e} &= \left[ mh - \frac{a \sin(ch)}{c^2} \right] - \left[ mg - \frac{a \sin(cg)}{c^2} \right] \\ &= \left[ me - \frac{a \sin(ce)}{c^2} \right] - \left[ ms - \frac{a \sin(cs)}{c^2} \right] \\ &= m(e-s)\ - \frac{a \sin(ce)}{c^2} + \frac{a \sin(cs)}{c^2} \\ &= \frac{a \cos(cs)}{c} (e-s)\ - \frac{a \sin(ce)}{c^2} + \frac{a \sin(cs)}{c^2} \end{align*}$