From Acceleration to Displacement (part 2)
In a previous post I showed how to analytically double integrate (or rather repeat integrate) a ![]() wave to arrive at displacement or position. Here I’ll make it a little more generic, by integrating a sum of
wave to arrive at displacement or position. Here I’ll make it a little more generic, by integrating a sum of ![]() waves, each with its own amplitude and phase. This exercise is motivated by the fact that any arbitrarily complex waveform can be expressed as the sum of a number of sinusoids, so this will allow us to obtain the exact displacement when the acceleration is arbitrarily complex, as long as we’re able to determine (through FFT perhaps) the sinusoids that make up the acceleration.
waves, each with its own amplitude and phase. This exercise is motivated by the fact that any arbitrarily complex waveform can be expressed as the sum of a number of sinusoids, so this will allow us to obtain the exact displacement when the acceleration is arbitrarily complex, as long as we’re able to determine (through FFT perhaps) the sinusoids that make up the acceleration.
We start with an acceleration defined as:
![]()
First integration, to obtain velocity:
(1) 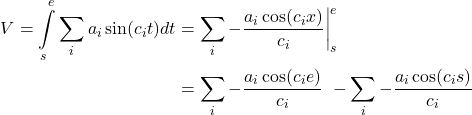
Let ![]() and then do the second integration, to obtain displacement or position.
and then do the second integration, to obtain displacement or position.
(2) ![Rendered by QuickLaTeX.com \begin{align*} D &= \int\limits_{g}^{h} \sum\limits_{i}{ - \frac{a_i \cos(c_i e)}{c_i}} \ - m\ de \\ &= \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2} - me \bigg|_g^h} \\ &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i h)}{c_i^2}} - mh \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i g)}{c_i^2}} - mg \right] \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-7d3277777343fb0ad9afd377e408b65a_l3.png)
Substitute everything back in (given ![]() and
and ![]() ), and simplify:
), and simplify:
(3) ![Rendered by QuickLaTeX.com \begin{align*} D &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i h)}{c_i^2}} - mh \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i g)}{c_i^2}} - mg \right] \\ &= \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2}} - me \right] - \left[ \sum\limits_{i}{-\frac{a_i \sin(c_i s)}{c_i^2}} - ms \right] \\ &= \sum\limits_{i}{-\frac{a_i \sin(c_i e)}{c_i^2}} \ - \sum\limits_{i}{-\frac{a_i \sin(c_i s)}{c_i^2}} + (s-e)\sum\limits_{i}{ - \frac{a_i \cos(c_i s)}{c_i}} \\ &= \sum\limits_{i}{\frac{a_i \sin(c_i s)}{c_i^2}} \ - \sum\limits_{i}{\frac{a_i \sin(c_i e)}{c_i^2}} + (e-s)\sum\limits_{i}{\frac{a_i \cos(c_i s)}{c_i}} \end{align*}](http://ebixio.com/blog/wp-content/ql-cache/quicklatex.com-1588dae166b76d154e41397796fe1f23_l3.png)
Finally, to take the phase of the signal into account, we would start with:
![]()
And end with:
![]()